반응형
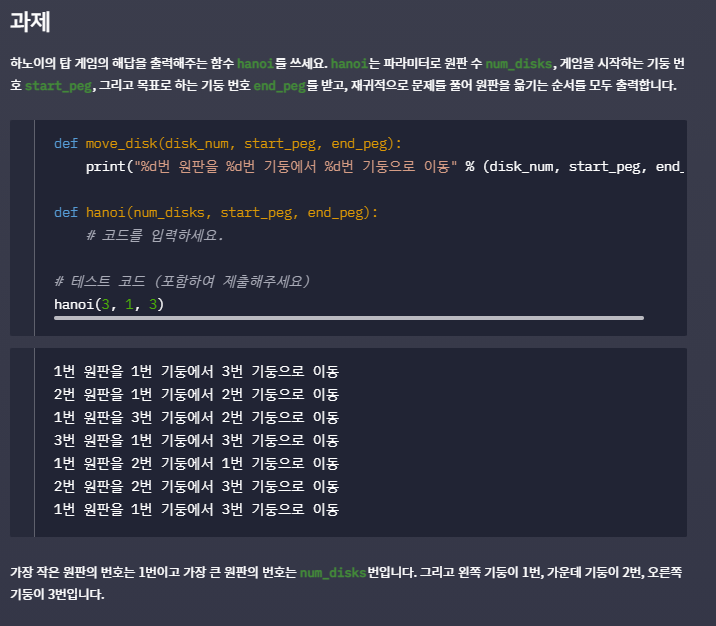
하노이 탑 문제를 보고 간단한 것 같은데 간단하지 않았다... 그래서 일단 수열을 풀듯 4번까지는 직접 그려가면서 생각해 보았다.
- 원판의 개수가 1개일 때, 1번 기둥에서 3번 기둥으로 옮기면 끝
- 원판의 개수가 2개일 때, 1번째 원판을 2번기둥으로 옮겨주고, 2번째 원판을 3번기둥으로 옮겨주고 1번째 원판을 3번째 기둥으로 옮겨준다.
- 원판의 개수가 3개일 때, 1번째와 2번째 원판을 2번기둥으로 옮겨주고, 3번째 기둥을 3번기둥으로 옮겨주고, 1번째와 2번째 기둥을 3번째 기둥으로 옮겨준다
- 원판의 개수가 4개일 때, 1,2, 그리고 3번째 원판을 2번 기둥으로 옮겨주고...
위의 과정을 통해 생각해보니 공통적으로 나오는 움직임을 찾았다.
- 1번 기둥에서 2번 기둥으로 옮기기
- 1번 기둥에서 3번 기둥으로 옮기기
- 2번 기둥에서 3번 기둥으로 옮기기
- 3번 기둥에서 2번 기둥으로 옮기기
즉 기본적으로 1번 기둥에서 3번 기둥으로 가는 것이 목표이다. <- base case
그런데 이를 위해선 자신보다 위에 있는 원판을 일단 3번이 아닌 다른 곳으로 옮겨야 한다 <- recursive case
3번이 아닌 다른 곳은
temp_peg = 6 - start_peg - end_peg 라고 놓으면,
2번에서 3번으로 가기위해 1번으로 옮기는 경우도 처리할 수 있다.
def move_disk(disk_num, start_peg, end_peg):
print("%d번 원판을 %d번 기둥에서 %d번 기둥으로 이동" % (disk_num, start_peg, end_peg))
def hanoi(num_disks, start_peg, end_peg):
# 코드를 입력하세요.
if num_disks == 0:
return
else:
other_peg = 6 - start_peg - end_peg
hanoi(num_disks-1, start_peg, other_peg)
move_disk(num_disks,start_peg,end_peg)
hanoi(num_disks-1, other_peg, end_peg)
반응형
'알고리즘 > 문제 풀이' 카테고리의 다른 글
| 2021-10-09 가장 가까운 거리 구하기 반영환 (0) | 2021.10.11 |
|---|---|
| 2021-10-09 두 뭉치의 곱의 최댓값 반영환 (0) | 2021.10.11 |
| 2021-10-07 이진탐색 재귀 반영환 (0) | 2021.10.11 |
| 2021-10-07 리스트 뒤집기 반영환 (2) | 2021.10.11 |
| 2021-10-05 각 자릿수의 합 반영환 (0) | 2021.10.11 |